lunes, 14 de octubre de 2013

2.1 Ecuación fundamental de la hidrostática

En el líquido en reposo, se aísla un volumen infinitesimal, formado por un prisma rectangular de base  \ A  y altura  \ dz .
Imaginemos un plano de referencia horizontal a partir del cual se miden las alturas en el eje z.
La presión en la base inferior del prisma es  \ p , la presión en la base superior es  \ p + dp . La ecuación del equilibrio en la dirección del eje z será:
\ p. A - (p + dp).A - \rho .g.A.dz =0
o sea:
\frac {dp} {\rho } = -g.dz
integrando esta última ecuación entre 1 y 2, considerando que  \ \rho = cte.  se tiene:
g(z_2 - z_1) = \frac {p_1 - p_2} {\rho }
o sea:
\frac {p_1} {\rho } +z_1.g = \frac {p_2} {\rho } +z_2.g
Considerando que 1 y 2 son dos puntos cualesquiera en el seno del líquido, se puede escribir la ecuación fundamental de la hidrostática del fluido incompresible en las tres formas que se muestran a continuación.

ECUACIÓN FUNDAMENTAL DE LA HIDROSTATICA DE FLUIDOS QUIETOS.


Primera forma de la ecuación de la hidrostática


\frac {p} {\rho } + z.g = y_1

La ecuación arriba es válida para todo fluido ideal y real, con tal que sea incompresible.

(Fluido ideal es aquel fluido cuya viscosidad es nula)

Segunda forma de la ecuación de la hidrostática

\frac {p} {\rho .g } + z = y_2
La constante y2 se llama 'altura piezométrica

Tercera forma de la ecuación de la hidrostática

\ p + \rho .g.z = y_3
Donde:
  • \ \rho  = densidad del fluido
  • \ p  = presión
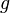  • \ g  = aceleración de la gravedad
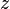  • \ z  = cota del punto considerado
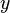  • \ y  = altura piezometrica



EJERCICIO:

Determine la presión a la que esta sometida en cada punto y calcular en cuantas veces supera a la que experimentaría en el exterior (Xveces=Psometida/Pexterior), sabiendo que la densidad del agua de mar es de 1,025.10^3 Kg/m^3 y que la presión atmosférica es de 1,01.10^2 KPa.
Respuesta:
Copio la respuesta de Yogel Mota (PQ003) que esta muy completa, solo que donde el coloco puntos yo colocaría comas, si quieren solo conocer los resultados de las dos preguntas de forma rápida lean el comentario de Elsa Belmonte (PQ001):
"Parte I: Presión a la que está sometida el submarinista en los tres puntos; a, b y c.
profundidad a= 10 m
profundidad b= 100 m
profundidad c = 10 km que al hacer la debida conversión a metros son: 10000 m.
usando la ecuación fundamental de la hidrostática en cada punto, y sabiendo que depende únicamente de la profundida a la cual se encuentra sumergido el submarinista, y que la presión externa ( presión atmosférica = 1.01 * 10^5 pascal por conversión de la unidad anterior que era Kpa), la densidad del agua de mar ( 1.025 * 10^3 kg/m^3) y la aceleración de gravedad (g)( 9,8 m/ s^2) son constantes, se tienen que los valores de esas presiones son:
Presion en a = 201450 Pa( pascales) en notación científica se tiene: 2.0145 * 10 ^5 Pa.
Presión en b = 1105500 Pa (pascales), en notación científica se tiene: 1.1055 * 10^6 Pa .
y Presión en c= 100551000 Pa ( pascales), en notación científica se tiene: 1.00551 * 10^8 Pa.
Parte II: veces que supera a la que experimentaría en el exterior.
x veces= P. sometida/ P. exterior; sustituyendo para cada uno de las presiones de los puntos a,b y c se tiene:
Xa( veces del punto a)= Pa/ P. atm. En consecuencia
Xa= 2.0145*10^5/ 1.01*10^5= 1.99 veces
Xb( veces del punto b)= Pb/ P. atm. En consecuencia
Xb= 1.1055*10^6/ 1.01*10^5= 10.94 veces
Xc ( veces del punto c)= Pc/P. atm. En consecuencia
Xc= 1.00551*10^8/ 1.01*10^5= 995.55 veces

APLICACIÓN:



Publicado por en

1 comentario:

Suscribirse a: Enviar comentarios (Atom)